Estimated Contributions in the WNBA

Introduction

Over the past year alone, the WNBA has achieved several notable milestones – from a new collective bargaining agreement to an eventful free agency period to an unprecedented virtual draft. Analytics has certainly been part of the recent evolution. Prior to the 2019 season, the league redesigned its web site, adopting the same structure as NBA.com and making lineup, on/off, and other statistics more readily accessible than ever before. While tracking and play-type data are still unavailable (the latter exists, but requires a Synergy subscription), there seems to be some investment in providing advanced stats to the masses.

In light of these developments, it’s as good a time as any to create an all-in-one metric that estimates player contributions on the court. Such work has obviously been done before. Basketball Reference, Kevin Pelton, and Jacob Goldstein all have WNBA versions of Win Shares (WS), Wins Above Replacement Player (WARP), and Player Impact Plus-Minus (PIPM), respectively. Nevertheless, the NBA has seen some exciting advancements lately with Kostya Medvedovsky’s DARKO, Daniel Myers’s Box Plus/Minus 2.0, and FiveThirtyEight’s RAPTOR, and I believe there’s value in researching whether some of their techniques can be applied to the WNBA.

This last point about applicability is worth emphasizing. Notwithstanding some similarities between the NBA and the WNBA, there are substantial nuances to each league that complicate adaptation. For instance, the WNBA has fewer teams that play fewer, shorter games. It’s also a younger league that has undergone numerous structural changes within a relatively brief period. It has switched from two 20-minute halves to four 10-minute quarters, moved the three point line back on two occasions, and experienced expansion, contraction, and franchise movements throughout its 23-year history.

Furthermore, players’ career arcs tend to be different. Four-year collegiate experiences are still common for WNBA players. Many of them play professionally overseas and have national-team obligations that take them out of the league. Personal considerations often lead to extended time away from the game, with Maya Moore and Skylar Diggins-Smith among just the latest examples. Overall, from an analyst’s perspective, these factors lead to smaller, more uneven sample sizes than what we typically see in the NBA, and they can make it challenging to transfer ideas from one league to the other.

Having said that, many approaches do, in fact, carry over to the WNBA, so the model below follows a familiar process from the NBA side:

1. Start with multi-season Regularized Adjusted Plus-Minus (RAPM).
2. Regress some combination of box-score, play-by-play, and on-court/off-court impact statistics against RAPM.
3. Apply a series of adjustments to adapt the model to a single-season setting.

The ensuing paragraphs provide details on each step, including areas where I draw inspiration from BPM, RAPTOR, PIPM, and Justin Willard’s Dredge.

Multi-Season RAPM

While foundational RAPM models conventionally span over a decade’s worth of NBA seasons, this approach is problematic in a WNBA setting. Among other things, it yields a very small sample of players, making it difficult to split the data for training and testing.

Instead, I adopt the BPM methodology and use three sets of 5-year RAPM values that cover the 2003 through 2017 seasons. These values result from ridge regressions with three defining characteristics that extend throughout the entire analysis.

First, player contributions on offense and defense are modeled separately. Down the line, we can see this separation play out in how certain features (e.g., rebounds) are divided into their offensive and defensive parts, as well as how defensive components are regressed more heavily toward replacement level than offensive components are.

Second, RAPM accounts for random variation in 3-point and free throw shooting — i.e., it’s “luck-adjusted.” Rather than using actual points when a 3-pointer or a free throw is taken, it utilizes expected points based on the shooter’s career average through the end of the season in which the possession is played.

Lastly, following the lead of Myers and James Brocato, RAPM is informed by a simple prior based on team quality and player workload. “Team quality” consists of offensive and defensive ratings that adjust for luck, game location, and opponent strength. “Workload” is defined as the percentage of a team’s total minutes in which a player is on the floor.

This version of RAPM, which I tested and found to produce better results than those without luck adjustment and prior information, provides the target variables for the weighted least squares regressions below. Like PIPM and RAPTOR, both the offensive and defensive models consist of a box score component (focusing on individual counting stats) and an on/off component (focusing on team performances with or without a player). Predictor variables are adjusted for team pace and presented as player totals per 40 minutes unless otherwise noted.

Box Score Components

The offensive component includes 13 variables, which can be grouped into six categories: workload, offensive responsibility, scoring, shot distribution, playmaking/creation, and rebounding. The defensive component is considerably more parsimonious, incorporating just four box score statistics. Altogether, they represent familiar concepts, though in some cases, they have certain nuances in how they are framed or implemented.

Workload

The amount (minutes per game) and the type (percentage of games as a starter) of playing time suggests player quality. As many analysts have previously noted, these are standard ways to incorporate some coaching assessments into a model.

Offensive Responsibility

This category includes both a conventional metric (usage rate) and a new metric (percentage of a team’s points that a player scores or assists while on the floor). Whereas the former works as one would expect, the latter has a negative coefficient. This counterintuitive result certainly raises some red flags — something I plan to examine closer in future work, even if just to engineer the feature a little better. But, for now, I leave it in the model as is, because it leads to better performance compared to other alternatives.

Ultimately, “percentage of points contributed” tempers the positive impact of players whose offensive value stems almost exclusively from assists. Think of playmakers who facilitate teammates’ scoring but take few shots of their own. Facilitation has its benefits (captured in the playmaking/creation category below, which focuses on assists), but they diminish when a player leans so heavily on passing that she declines to take available shots. In other words, a high percentage of points contributed can be a net negative if it comes with a low usage rate.

Scoring

Volume and efficiency are captured via points and Dredge’s points over average. The inclusion of both metrics (as opposed to just one or the other) improves model performance, and this particular combination works better than those that use true shooting, effective field goal, or other such percentages.

Shot Distribution

This category focuses on the three “Moreyball” areas where offenses can generate scoring efficiency: 3-point attempts, free throw attempts, and field goal attempts in the restricted area. The first two have positive coefficients, and apart from being high-value opportunities, they bring additional benefits through spacing and foul-drawing.

By contrast, the rim attempts variable has a negative coefficient. In part, it’s because the value brought by players who take plenty of shots in the restricted area is likely manifesting itself elsewhere. Prolific rebounders, for example, gravitate toward the basket, and offensive boards have a positive coefficient. Furthermore, rim attempts tend to rely on others’ creation, as these shots are highly correlated with being assisted. Such offensive dependence lowers the scorer’s value.

Playmaking/Creation

To elaborate on this last point, assists and assisted field goals have positive and negative coefficients, respectively. The model follows the RAPTOR methodology of weighting each assist by the expected points associated with the zone where the shot occurs. So, for example, assists at the rim are worth more than those in the midrange, while assisted field goals behind the arc are debited more than those in the paint. Perhaps there are better ways to estimate weights, but it’s clear that not all dimes are created equal, and the model with “enhanced assists” outperforms alternatives with raw counts.

On the other hand, turnovers are presented as is. Dredge includes an extra penalty for live-ball turnovers, but in my analysis, this addition does not lead to substantially better results, so I settled for the simpler approach. It is certainly an area that requires closer inspection down the line.

Rebounding

Similarly, offensive boards are kept in their raw form. RAPTOR makes a variety of different adjustments, including those for the location of the shot that precedes the rebound. I save them for future consideration and go with simplicity instead.

Defense

As with many other models, the defensive component suffers from a relatively limited pool of available data. It consists of just defensive rebounds, steals, blocks, and personal fouls — all from standard box scores.

Offensive fouls drawn is among the statistics derived from play-by-play logs that often augment defensive models. Unfortunately, it’s only available from the 2006 season onward. While it picks up some signal, it’s not definitive enough for me to justify having two different models, at least not in the first iteration of this work.

Likewise, differentiating block types (specifically, those at the rim and in the paint) has its benefits, according to Dredge. But, for my purposes, it hardly improves model performance, so I opted to leave it out. Again, this area warrants further study down the line.

On/Off Components

The offensive and defensive components are constructed in the same way here, adopting the RAPTOR approach to estimate player impact on team ratings (i.e., points scored and allowed per 100 possessions). Specifically, each component has three variables, all of which are adjusted for luck and opponent strength:

1. Team rating when the player is on the floor;
2. Team rating when courtmates are on the floor without the player — a weighted average based on (a) the number of possessions that a courtmate has with the player multiplied by (b) the number of possessions that a courtmate has without the player; and
3. The same team rating as in #2, but applied to the courtmates’ other courtmates.

The RAPTOR summary has more details on how the three variables work together. Overall, my own tests confirm that this approach outperforms standard on/off ratings, as well as other alternatives in which on/off numbers are either added to or replaces one of the variables.

Adjustments

To finalize the two sets of box score and on/off components, three adjustments are applied. They draw from the methods employed by PIPM and BPM, with the objective of adapting the numbers to a single-season environment.

First, the components are regressed toward league average (0 points per 100 possessions). This adjustment uses the square root of a player’s total minutes divided by the maximum number of available minutes in a season. Note that the denominator has changed numerous times, as the WNBA has tinkered with its schedule.

Second, the components are regressed toward replacement level. This adjustment amounts to 250 possessions at -1.7 points per 100 possessions on offense and 500 possessions at -0.3 points per 100 possessions on defense. The replacement-level figures are fairly standard for the NBA, and while they seem to work for the WNBA, they need to be examined more closely in the future. Nonetheless, this modification, like the preceding one, helps account for variance in small samples.

Lastly, after the regressed components are assembled, a “constant” team adjustment is added. This way, when individual players’ estimated contributions are combined, the sum is equal to the team’s adjusted rating for the season.

Evaluating the Model

Ideally, the model would be evaluated by determining how well it predicts future team performance (win percentage, margin of victory, net rating, etc.). Unfortunately, even under the best circumstances in the NBA, this test has its shortcomings, since there are only 30 teams in the first place, and player movement (the entry of rookies, the departure of retired players, etc.) introduces quite a bit of noise. Such issues are exacerbated in the WNBA, especially with just eight seasons available out of sample.

As an alternative, we can assess how well the model correlates with luck-adjusted, single-season RAPM the following year. To be sure, RAPM itself has its own problems, but it at least has certain properties that make it useful for our purposes.

The table below summarizes the average R-squared between the model, which I simply call “Estimated Contribution” (EC), and future RAPM. The analysis covers the 1997-2002 and 2018-2019 WNBA seasons. For comparison, I also include results for a standard benchmark (which distributes team ratings equally among all players on the roster), luck-adjusted RAPM, and PIPM.

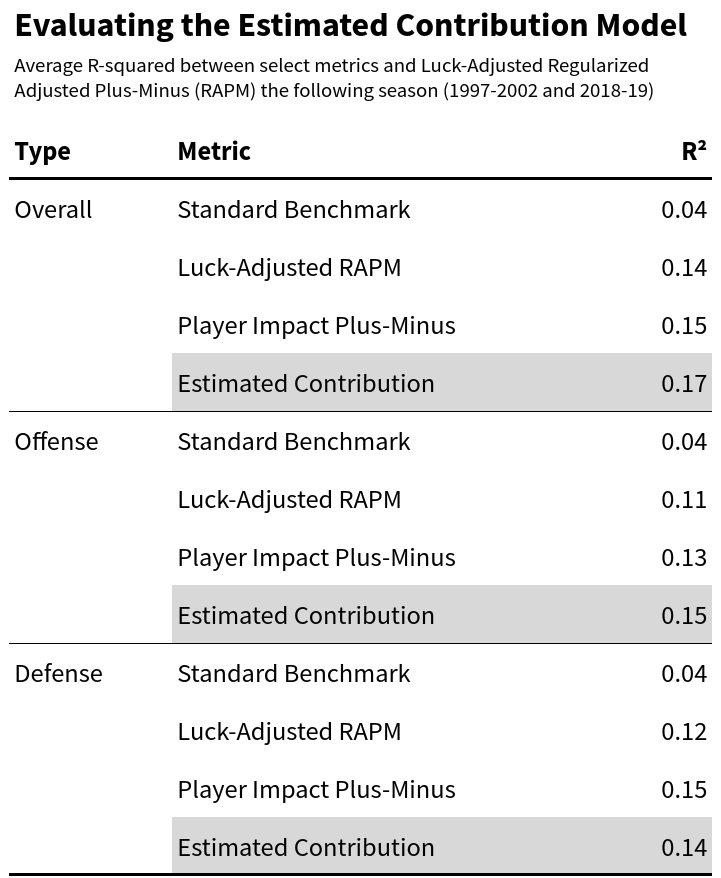
Though I would hardly view it as definitive, EC outperforms the standard benchmark and luck-adjusted RAPM. It edges PIPM overall and on offense, while trailing on defense. At a minimum, it appears competitive with one of the notable public metrics.

Top Performances

In closing, it’s worth examining the best single-season performances according to EC. While I generally discourage the use of all-in-one metrics for player rankings, I believe it’s important to analyze patterns and see whether they make sense.

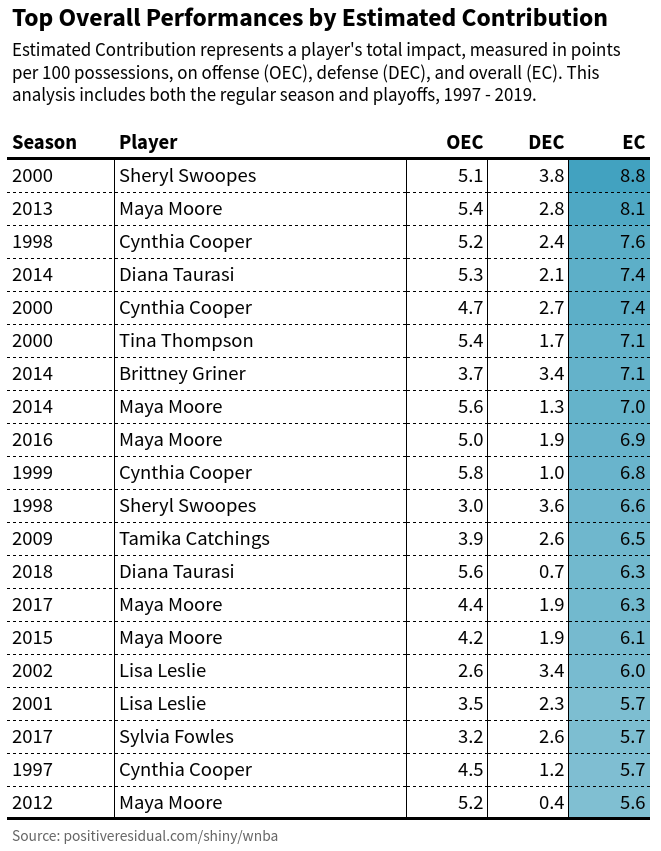
Maya Moore and Cynthia Cooper occupy half of the top 20 overall performances, reflecting dominant multi-season runs that other analyses have also found to be noteworthy. Six Most Valuable Player campaigns are represented, and two other MVP recipients make appearances.

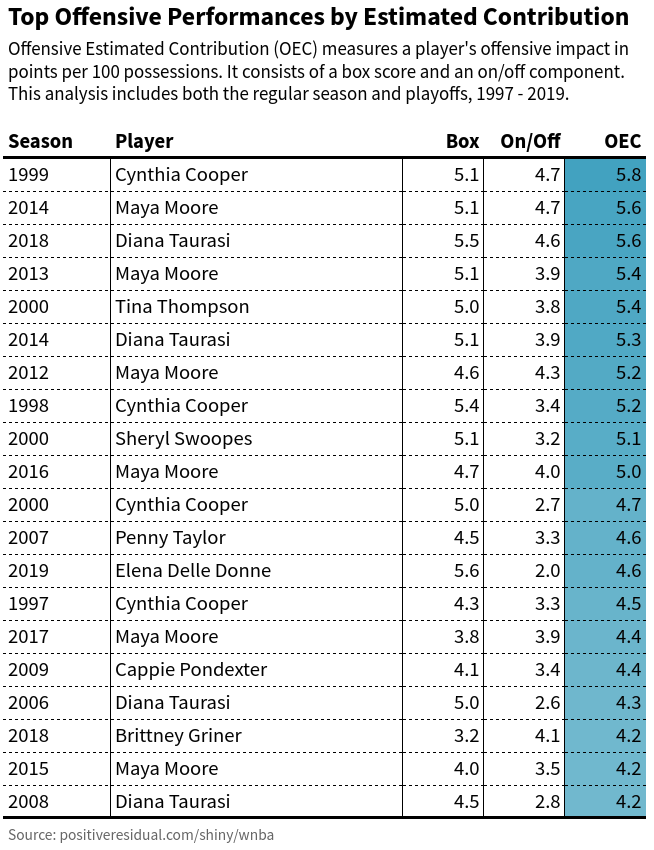
In addition to Moore and Cooper, Diana Taurasi has four seasons on the top 20 offensive performances. Her box score contributions have consistently been stellar throughout her career: efficient shooting on high usage; impressive volume of both 3-pointers and free throws; and strong assist rates with an incredible ability to create her own shots.

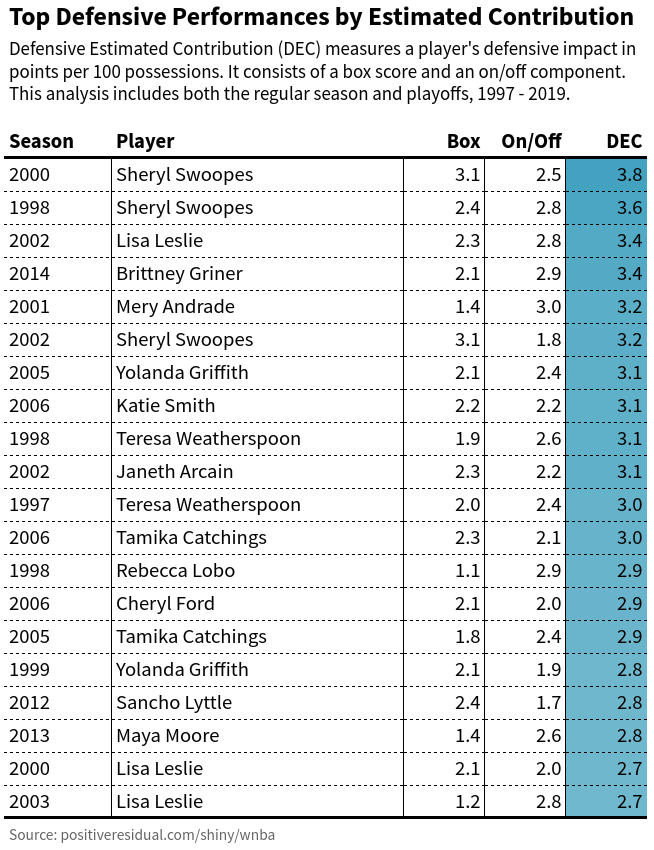
The top 20 defensive performances include eight Defensive Player of the Year campaigns. Of the seven players who have won this award multiple times, five are on the list.

To go beyond the top 20, you can visit the WNBA Dashboard, where the entire table is posted. Altogether, despite some clear areas for future improvement, EC appears to yield intuitive results in addition to performing reasonably well and leveraging recent NBA literature. But, above all, it adds to the growing WNBA conversation at a critical juncture in its history.